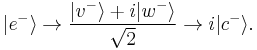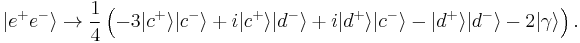Hardy's paradox
Hardy's paradox is a thought experiment in quantum mechanics devised by Lucien Hardy[1][2] in which a particle and its antiparticle may interact without annihilating each other. The paradox arises in that this may only occur if the interaction is not observed and so it seemed that one might never be able to confirm this.[3]
Experiments[4][5] using the technique of weak measurement[3] have studied an interaction of polarized photons and these have demonstrated that the phenomenon does occur. However, the consequence of these experiments maintain only that past events can be inferred about after their occurrence as a probabilistic wave collapse. These weak measurements are considered by some to be an observation themselves, and therefore part of the causation of wave collapse, making the objective results only a probabilistic function rather than a fixed reality.
Setup description and the results
The basic building block of Hardy’s thought experiment are two Mach–Zehnder interferometers for quantum particles. Each interferometer is tuned so that when operating individually particles only ever exit to the same particle detector. For example, for the right hand side interferometer, when operating alone, particles entering in arm 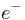 would always exit in arm
would always exit in arm 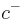 :
:
In the actual experiment the interferometers are arranged so that part of their arms overlap as shown in the diagram. If the amplitude for the particle in one arm, say 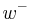 , were to be obstructed by a second particle in
, were to be obstructed by a second particle in 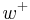 that collides with it, only the
that collides with it, only the  amplitude would reach the second beam splitter, and would split into arms
amplitude would reach the second beam splitter, and would split into arms 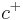 and
and 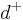 with equal amplitude. The detection of a particle in
with equal amplitude. The detection of a particle in 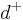 would thus indicate the presence of the obstructing particle without the latter being affected. For this reason, this scheme was named interaction-free measurement.
would thus indicate the presence of the obstructing particle without the latter being affected. For this reason, this scheme was named interaction-free measurement.
If both the electron and the positron take arms w in their respective interferometers, they will annihilate with certainty to produce gamma radiation: 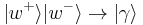 . Therefore the presence of either particle in its
. Therefore the presence of either particle in its  arm will affect the other’s interferometer output:
arm will affect the other’s interferometer output:
The situation can be analyzed in terms of two simultaneous interaction-free measurements: from the point of view of the interferometer on the left, a click at 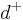 implies the presence of the obstructing electron in
implies the presence of the obstructing electron in 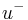 . Similarly, for the interferometer on the right, a click at
. Similarly, for the interferometer on the right, a click at 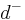 implies the presence of the positron in
implies the presence of the positron in 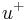 . Indeed, every time a click is recordered at
. Indeed, every time a click is recordered at 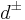 the other particle is found in
the other particle is found in 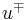 . If we assume the particles are independent (described by local hidden variables), we conclude that they can never emerge simultaneously in
. If we assume the particles are independent (described by local hidden variables), we conclude that they can never emerge simultaneously in 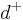 and
and 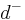 . This would imply that they were in
. This would imply that they were in 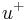 and
and 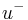 , which cannot occur because of the annihilation process.
, which cannot occur because of the annihilation process.
A paradox then arises because sometimes the particles do emerge simultaneously at 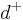 and
and 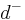 (with probability p=1/16). Quantum mechanically, the
(with probability p=1/16). Quantum mechanically, the 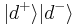 term arises, in fact, from the nonmaximally entangled nature of the state just before the final beam splitters.
term arises, in fact, from the nonmaximally entangled nature of the state just before the final beam splitters.
References
- ^ Hardy, Lucien (1992). "Quantum mechanics, local realistic theories, and Lorentz-invariant realistic theories". Physical Review Letters 68 (20): 2981–2984. Bibcode 1992PhRvL..68.2981H. doi:10.1103/PhysRevLett.68.2981. PMID 10045577.
- ^ Hardy, Lucien (1993). "Nonlocality for two particles without inequalities for almost all entangled states". Physical Review Letters 71 (11): 1665–1668. Bibcode 1993PhRvL..71.1665H. doi:10.1103/PhysRevLett.71.1665. PMID 10054467.
- ^ a b Mae-Wan Ho (2008). "Quantum Entanglement and Coherence". The Rainbow and the Worm. p. 294. ISBN 9789812832597. http://books.google.com/?id=zPH2L5sN1hsC&pg=PA294&dq=%22Hardy%27s+paradox%22. Retrieved 2009-03-19.
- ^ Lundeen, J. S.; Steinberg, A. M. (2009). "Experimental Joint Weak Measurement on a Photon Pair as a Probe of Hardy’s Paradox". Physical Review Letters 102 (2): 020404–000001. Bibcode 2009PhRvL.102b0404L. doi:10.1103/PhysRevLett.102.020404.
- ^ Yokota, K.; Yamamoto, T.; Koashi, M.; Imoto, N. (2009). "Direct observation of Hardy's paradox by joint weak measurement with an entangled photon pair". New Journal of Physics 11 (3): 033011. Bibcode 2009NJPh...11c3011Y. doi:10.1088/1367-2630/11/3/033011.